Մաթեմատիկա

Մաթեմատիկա (հին հունարեն՝ μάθημα՝ գիտություն, ուսումնասիրություն բառից, հայերեն անվանումն է՝ Ուսողություն[1]), գիտություն կառուցվածքների, հաջորդականությունների և հարաբերությունների մասին։ Պատմականորեն ձևավորվել և զարգացել է իրական առարկաները հաշվելու, դրանք չափելու և դրանց ձևերը նկարագրելու գործողությունների հիման վրա[2]։
Մաթեմատիկական օբյեկտներն ստեղծվում են իրական կամ այլ մաթեմատիկական օբյեկտների հատկություններն իդեալականացնելու և հատուկ լեզվով դրանք գրառելու ճանապարհով։ Մաթեմատիկան բնական գիտությունների շարքին չի դասվում, սակայն լայնորեն կիրառվում է այդ գիտություններում՝ ինչպե՛ս ճշգրիտ բովանդակություն ներկայացնելու, այնպե՛ս էլ նոր արդյունք ստանալու համար[3]։ Մաթեմատիկան հիմնարար գիտություն է, որի միջոցով այլ գիտություններում բովանդակությունը ներկայացվում է մեկ միասնական լեզվով՝ այդ կերպ օգնելով գիտության տարբեր ճյուղերին ընդհանուր օրենքները գտնելու հարցում։
Մաթեմատիկոսները նմուշներ են որոնում և դրանք օգտագործում նոր վարկածներ ձևակերպելու համար։ Մաթեմատիկոսները ենթադրության ճիշտ կամ սխալ լինելը որոշում են մաթեմատիկական ապացույցի միջոցով։ Երբ մաթեմատիկական կառուցվածքներն իրական երևույթների հաջողված մոդելներ են, մաթեմատիկական դիտարկումները կարող են ապահովել բնության վերաբերյալ պատկերացումները և կանխատեսումները։ Աբստրակցիայի և տրամաբանության օգնությամբ մաթեմատիկան զարգացել է հաշվարկներից, չափումներից և ուրվագծերի և ֆիզիկական օբյեկտների շարժումների համակարգված ուսումնասիրությունից։ Պրակտիկ մաթեմատիկան մարդկային գործունեություն էր դեռևս գրառումների ժամանակներից։ Մաթեմատիկական խնդիրների լուծումները գտնելու տևողությունը կարող է տարիներ և նույնիսկ դարեր պահանջել։
Խիստ փաստարկներ առաջին անգամ հայտնվել են հունական մաթեմատիկայում, հատկապես Էվկլիդեսի «Տարրեր» աշխատությունում։ Ջուզեպե Պեանոյի (1858-1932), Դավիդ Հիլբերտի (1862-1943) և այլոց կողմից մաթեմատիկայի հիմունքների ստեղծումից ի վեր մաթեմատիկական հետազոտությունը դիտարկվում է որպես համապատասխանաբար ընտրված աքսիոմներից և սահմանումներից խիստ դեդուկցիայով դուրս բերված ճշմարտություն։ Մինչև Վերածնունդ մաթեմատիկան զարգացել է դանդաղ, այնուհետ նորարարական գիտական հայտնագործությունները բերել են մաթեմատիկական հայտնագործությունների արագ աճին, ինչը շարունակվում է մինչ օրս[4]։
Գալիլեո Գալիլեյը (1564-1642) ասել է. «Տիեզերքը հնարավոր չէ կարդալ, քանի դեռ մենք չենք սովորել լեզուն և չենք ծանոթացել սիմվոլներին, որոնցով դրանք գրված են։ Այն գրված է մաթեմատիկական լեզվով, իսկ տառերն այն եռանկյունները, շրջանները և երկրաչափական այլ պատկերներն են, առանց որոնց անհնար է հասկանալ մի բառ։ Առանց դրանց՝ մարդը խճճվում է մութ լաբիրինթոսում»[5]։ Կառլ Գաուսը (1777–1855) մաթեմատիկային անդրադարձել է որպես «Գիտությունների թագուհի»[6]։ Բենիամին Փիրսը (1809-1880) մաթեմատիկան անվանել է «գիտություն, որն անհրաժեշտ եզրահանգումներ է անում»[7]։ Դավիդ Հիլբերտը մաթեմատիկայի մասին ասել է. «Մենք այստեղ չենք խոսում որևէ իմաստով կամայականությունների մասին։ Մաթեմատիկան կամայականորեն սահմանված կանոններով խաղ չէ։ Այն ավելի շուտ ներքին կոնցեպտուալ համակարգ է, որը կարող է լինել միայն այդպիսին և ոչ այլ կերպ»[8]։ Ալբերտ Այնշտայնը (1879-1955) հայտարարել է. «Քանի որ մաթեմատիկայի օրենքները վերաբերում են իրականությանը, դրանք չեն կարող ճշգրիտ լինել, և քանի որ դրանք որոշակի են, դրանք չեն կարող վերաբերել իրականությանը»[9]։
Մաթեմատիկան անհրաժեշտ է բազմաթիվ բնագավառներում՝ ներառյալ բնագիտությունը, ճարտարագիտությունը, բժշկությունը, ֆինանսները և հասարակագիտությունը։ Կիրառական մաթեմատիկան կատարելապես նոր ուղղությունների հիմք դրեց, ինչպիսիք են վիճակագրությունն ու խաղերի տեսությունը։ Մաթեմատիկոսները ներգրավված են նաև մաքուր մաթեմատիկայում (մաթեմատիկան հենց մաթեմատիկայի համար)` առանց որևէ կիրառության։ Մաքուր մաթեմատիկան կիրառական մաթեմատիկայից առանձնացնող հստակ սահման չկա, հաճախ հանդիպում են կիրառություններ, որոնք սկսվել են որպես մաքուր մաթեմատիկա[10]։
Պատմություն
Մաթեմատիկայի պատմությունը կարելի է դիտել որպես մշտապես աճող աբստրակցիաների շարք։ Առաջին աբստրակցիան, որ հավանաբար թվերի մեջ էր[11], որ երկու խնձորների հավաքածուն և երկու նարինջների հավաքածուն (օրինակ) ընդհանուր ինչ որ բան ունեն, մասնավորապես տարրերի քանակը։


Ինչպես վկայում են ոսկորների վրայի նշանները, նախապատմական մարդիկ ֆիզիկական օբյեկտները հաշվելու հետ մեկտեղ, կարողանում էին նաև հաշվել աբստրակտ թվերը՝ ինչպես ժամեր – օրեր, եղանակներ, տարիներ.[12]
Ավելի բարդ մաթեմատիկայի օգտագործման ապացույցներ չեն հայտնաբերվել մինչ 3000 մ․ թ․ ա․, երբ բաբելոնացիները և եգիպտացիները հարկման և այլ ֆինանսական հաշվարկների, շենքերի և շինարարության, ինչպես նաև աստղագիտության համար սկսեցին օգտագործել թվաբանություն, հանրահաշիվ և երկրաչափություն[13]։ Մաթեմատիկան ամենից վաղ օգտագործում էին առևտրի, հողաչափումների, նկարչության և տեքստիլ ձևերի մեջ։
Բաբելոնյան մաթեմատիկայում, տարրական մաթեմատիկան (գումարում, հանում, բազմապատկում և բաժանում) առաջինը հայտնաբերվել է հնագիտական գրվածքներում։ Թվերը, որ նախորդել էին գրերին և թվային համակարգերին շատ էին և բազմազան, առաջին հայտնի գրավոր թվերը ստեղծվել էին եգիպտացիների կողմից, Միջին դարերի Եգիպտոսի այդպիսի տեքստերից է մաթեմատիկական պապիրուսները։
Մ․ թ․ ա․ 600 և 300 Հին հույները սկսել էին մաթեմատիկայի համակարգված ուսումնասիրություն իրենց իսկ՝ Հունական մաթեմատիկայով[14]։

Իսլամի Ոսկե դարի ընթացքում, հատկապես 9-րդ և 10-րդ դարերում, մաթեմատիկայում հունական մաթեմատիկայի վրա հիմնված բազում կարևոր հայտնագործություններ կատարվեցին․ դրանց մեծ մասը կատարվեցին պարսիկ մաթեմատիկոսների՝ Ալ-Խորեզմիի, Օմար Խայամի և Շարաֆ Ալ-Տուսիի կողմից։
Այդ ժամանակներից ի վեր մաթեմատիկան մեծապես ընդլայնվել է, և մաթեմատիկայի և գիտության միջև պտղաբեր համագործակցություն է հաստատվել, ի օգուտ երկուսի։ Մաթեմատիկական հայտնագործությունները շարունակվում են և այսօր։ Ըստ Միխայել Սևրյուկի (Ամերիկյան Մաթեմատիկական Հանրության Տեղեկագրում հունվարի 2006), "Mathematical Reviews տվյալների բազայում 1940 թվականից ի վեր (ՄՏ-ի առաջին տպագրությունից) գրսնցվսծ հոդվածների և գրքերի քանակը գերազանցում է 1.9 միլիոն, և ավելի քան 75 հազար ավելանում է ամեն տարի։ Այս օվկիանոսի աշխատանքների գերակշիռ մասը նոր մաթեմատիկական թեորեմներ են և դրանց ապացույցները"։[15]
Ծագումնաբանություն
Մաթեմատիկա բառը սկիզբ է առնում հին հունարեն μάθημα (máthēma) բառից, որ նշանակաում է "այն, ինչ սերտած է"[16], "այն, ինչ պետք է իմանալ", հետևաբար նաև "ուսում" և "գիտություն", և ժամանակակից հունարենով պարզապես "դաս"։ máthēma բառը ծագում է μανθάνω (manthano), ժամանակակից հունարենով՝ μαθαίνω (mathaino) բառից, երկուսն էլ նշանակում են "սովորել"։ Հունաստանում "մաթեմատիկա" բառն ավելի նեղ տեխնիկական "մաթեմատիկական ուսումնասիրություն" իմաստն ունի և ուներ նույնիսկ Դասական ժամանակաշրջանում[17]։ Դրա ածականը՝ μαθηματικός (mathēmatikós) բառը, ունի "ուսմանը վերաբերող" կամ "աշխատասեր" իմաստները. այն հետագայում նաև "մաթեմատիկական" իմաստը ստացավ։ Մասնավորապես, μαθηματικὴ τέχνη (mathēmatikḗ tékhnē), լատին․՝ ars mathematica, նշանակում է "մաթարվեստ":
Նմանապես, մտքի երկու գլխավոր դպրոցներից մեկը՝ Պյութագորասականություն, հայտնի էր որպես mathēmatikoi (μαθηματικοί), որ ավելի շուտ նշանակում է "ուսուցիչներ", քան "մաթեմատիկոսներ" ժամանակակից իմաստով։
Լատիներենում և անգլերենում մինչ 1700-ականները մաթեմատիկա տերմինը ավելի շուտ "աստղագիտություն" էր նշանակում, քան "մաթեմատիկա". իմաստն աստիճանաբար փոխվեց ներկայիս նշանակությանը մոտավորապես 1500-ից 1800-ականներին։ Սա հանգեցրեց մի քանի սխալ թարգմանությունների․ վառ օրինակ է Սուրբ Օգոստինիոսի` աստղագետներին ուղղված տխրահռչակ նախազգուշացումը, որ քրիստոնjաները պետք է հեռու մնան մաթեմատիկայից, նկատի ունենալով աստղագիտությունը, որը սխալմամբ հասկացվել էր որպես մաթեմատիկոսների դատապարտում[18]։
Մաթեմատիկայի սահմանում

Արիստոտելը մաթեմատիկան սահմանում էր որպես «քանակի գիտություն», և այս սահմանումը գերակշռում էր մինչ 18-րդ դարը[19]։ 19-րդ դարից սկսած, երբ մաթեմատիկայի ուսումնասիրությունը խիստ աճեց և սկսեց վերաբերել այնպիսի աբստրակտ թեմաների, ինչպես խմբերի տեսությունը և պրոյեկտիվ երկրաչափությունն են, որոնք քանակի և չափման հետ հստակ առնչություն չունեն, մաթեմատիկոսներն ու փիլիսոփաները սկսեցին բազում նոր սահմանումներ առաջարկել[20]։ Այս սահմանումներից որոշները ընդգծում են մաթեմատիկայի դեդուկտիվ բնույթը, որոշները՝ վերացականությունը, որոշներն էլ ընդգծում են մաթեմատիկայի կոնկրետ թեմաներ։ Այսօր նույնիսկ մաթեմատիկոսների շրջանակում մաթեմատիկայի սահմանման միասնական կարծիք գոյություն չունի[21]։ Նույնիսկ միասնական կարծիք չկա՝ մաթեմատիկան արդյոք արվեստ է, թե գիտություն[22]։ Շատ պրոֆեսիոնալ մաթեմատիկոսներ հետաքրքրված չեն մաթեմատիկայի սահմանմամբ կամ համարում են, որ անհնար է այն սահմանել[21]։ Ոմանք պարզապես ասում են․ «Մաթեմատիկան այն է, ինչ մաթեմատիկոսներն անում են[21]։» Մաթեմատիկայի սահմանման երեք առաջատար տեսակներն են՝ լոգիցիզմ, ինտուիցիոնիզմ և ֆորմալիզմ, որոնցից յուրաքանչյուրը պատկանում է փիլիսոփայական մտածողության տարբեր դպրոցների[23]։ Երեքն էլ լուրջ խնդիրներ ունեն, ոչ մեկը լայն տարածում չի ստացել, և հաշտեցումը թվում է անհնար[23]։
Մաթեմատիկայի վաղ սահմանումը տրամաբանական տերմիններով տրվել է Բենջամին Պերսի «Գիտություն, որ անհրաժեշտ եզրակացություններ է անում» գրքում (1870)[24]։ Բերտրան Ռասելը և Ալֆրեդ Նորթ Ուայտհեդը Principia Mathematica աշխատությունում առաջադրեցին փիլիսոփայական ծրագիր, հայտնի որպես լոգիցիզմ, և փորձեցին ապացուցել, որ մաթեմատիկական բոլոր հասկացությունները, պնդումները և սկզբունքները կարող են սահմանվել և ապացուցվել ձևական տրամաբանության տերմիններով։ Մաթեմատիկայի տրամաբանական սահմանումը Ռասելինն է․ «Ողջ Մաթեմատիկան ձևական տրամաբանություն է» (1903)[25]։
Մաթեմատիկայի ինտուիցիոնիստական սահմանումը զարգացել էր հոլանդացի մաթեմատիկոս Լ.Ե.Ջ. Բրաուերի փիլիսոփայությունից, ով մաթեմատիկան նույնացնում էր որոշակի մտավոր ֆենոմենի հետ։ Ինտուիցիոնիստական սահմանման օրինակ է՝ «Մաթեմատիկան մտավոր գործունեություն է, որ բաղկացած է մեկը մյուսին հաջորդող գործողությունների շարքից»[23]։ Ինտուիցիոնիզմի առանձնահատկությունն այն է, որ այն մերժում է որոշակի մաթեմատիկական գաղափարներ, որոնք ըստ այլ սահմանումների համարվում են վավեր։ Մասնավորապես, երբ այլ մաթեմատիկական փիլիսոփայություններ թույլ են տալիս ապացուցվող օբյեկտներին գոյություն ունենալ, նույնիսկ եթե դրանք չեն կարող կառուցվել, ինտուիցիոնիզմը միայն թույլատրում է մաթեմատիկական օբյեկտներ, որոնք հնարավոր է կառուցել։
Մաթեմատիկայի ֆորմալիստական սահմանումները այն ներկայացնում են սիմվոլներով և գործողություններ կատարելու կանոններով։ Հասկել Կարին մաթեմատիկան սահմանել էր պարզ՝ որպես «ֆորմալ համակարգերի գիտություն»[26]։ Ֆորմալ համակարգը սիմվոլների կամ տողերի և տողերից բանաձևեր կազմելու որոշ կանոնների բազմություն է։ Ֆորմալ համակարգերում աքսիոմ բառը հատուկ իմաստ ունի, որը տարբեր է «ինքնին ակնհայտ ճշմարտություն» սովորական իմաստից։ Ֆորմալ համակարգերում աքսիոմը տվյալ համակարգում ներառված տողերի կոմբինացիա է՝ առանց համակարգի կանոնների օգտագործման անհրաժեշտության։
Մաթեմատիկան որպես գիտություն

Գերմանացի մաթեմատիկոս Կառլ Գաուսը մաթեմատիկան անվանել է «Գիտությունների թագուհի»[6] Բոլորովին վերջերս Մարկուս դյու Սուտոյը մաթեմատիկան անվանել է «Գիտության թագուհի ... գիտական հայտնագործությունների գլխավոր շարժիչ ուժը»[27]։ Լատիներեն «Regina Scientiarum» բնօրինակում, ինչպես նաև գերմաներեն «Königin der Wissenschaften» տարբերակի դեպքում գիտություն բառը նշանակում է «գիտելիքի դաշտ», որը «գիտություն» բառի սկզբնական իմաստն էր անգլերենում։ Այս իմաստով մաթեմատիկան նաև գիտելիքի դաշտ է։ Բեկոնի մեթոդի, որը հակադրում էր բնական գիտությունը սխոլաստիկային (Առաջին սկզբունքներում ներկայացված Արիստոտելի մեթոդ), զարգացմանը հետևեց «Գիտության» իմաստի սահմանափակումը բնական գիտության։ Էմպիրիկ փորձարկումների և դիտարկումների դերը մաթեմատիկայում, համեմատած բնական գիտությունների՝ կենսաբանության, քիմիայի կամ ֆիզիկայի, աննշան է։ Ալբերտ Այնշտայնը հայտարարել է. «Քանի որ մաթեմատիկայի օրենքներն իրականությանն են վերաբերում, դրանք հավաստի չեն. քանի որ դրանք ճշգրիտ են, ապա դրանք չեն վերաբերում իրականությանը[9]»:
Շատ փիլիսոփաներ կարծում են, որ մաթեմատիկան փորձով հնարավոր չէ հերքել, և ուստի, ըստ Կարլ Փոփերի սահմանման, այն գիտություն չէ[28]։ Այնուամենայնիվ, 1930-ականներին Գյոդելի ոչ լրիվության թեորեմը շատ մաթեմատիկոսների համոզեց, որ մաթեմատիկան չի կարելի սեղմել մինչև միայն տրամաբանության, և Կարլ Փոփերը եզրակացրեց, որ "մաթեմատիկայի տեսությունների մեծ մասը, ինչպես ֆիզիկան և կենսաբանությունը, հիպոթետիկա –դեդուկցիոն են։ Հետևաբար մաքուր մաթեմատիկան ավելի մոտ է բնական գիտություններին, որոնց հիպոթեզները ենթադրություններ են։"[29] Այլ մտածողներ, մասնավորապես Իմրե Լակատոսը, հերքելիության տարբերակը կիրառել են հենց մաթեմատիկայում։
Այլընտրանքային տեսակետ կա, որ կոնկրետ գիտական ոլորտներ (օրինակ՝ տեսական ֆիզիկա) մաթեմատիկա են աքսիոմներով, որոնք իրականությանն են համապատասխանեցված։ Մաթեմատիկան շատ ընդհանրություններ ունի ֆիզիկական գիտությունների բազմաթիվ բնագավառների հետ, հատկապես ենթադրությունների տրամաբանական հետևությունների հետազոտության։ Ինտուիցիան և փորձարկումները հիպոթեզի ձևակերպման մեջ դեր ունեն թե՛ մաթեմատիկայում, թե՛ այլ գիտություններում։ Կիրառական մաթեմատիկան շարունակում է բարձրացնել իր կարևորությունը մաթեմատիկայի ներսում, իսկ հաշվելիության և մոդելավորման դերը աճում է գիտության բազմաթիվ բնագավառներում։
Ոգեշնչում, մաքուր և կիրառական մաթեմատիկա և գեղագիտություն
Մաթեմատիկան ծագում է տարբեր տեսակի խնդիրներից։ Սկզբում դրանք հայտնաբերվել են առևտրի, հողաչափության, ճարտարապետության և ավելի ուշ աստղագիտության մեջ. այսօր բոլոր գիտությունները մաթեմատիկոսների հետազոտության պրոբլեմներ են առաջադրում, և շատ պրոբլեմներ ի հայտ են գալիս հենց մաթեմատիկայում։ Օրինակ՝ ֆիզիկոս Ռիչարդ Ֆեյմանը, օգտագործելով մաթեմատիկական հիմավորումների և ֆիզիկական պատկերացումների համադրությունը, հայտնագործեց քվանտային մեխանիկայի ինտեգրալ բանաձևը, և արդի լարերի տեսությունը, դեռևս զարգացող գիտական տեսություն, որը փորձում է միավորել բնության չորս հիմնարար փոխազդեցությունները, շարունակում է ոգեշնչել մաթեմատիկան։
Որոշ մաթեմատիկոսներ վերաբերում են միայն այն բնագավառին, որն այն առաջացրել է։ Սակայն, շատ հաճախ, մի բնագավառում առաջացած մաթեմատիկան օգտակար է դառնում շատ ոլորտներում և միանում է մաթեմատիկական հասկացությունների ընդհանուր ֆոնդին։ Հաճախ տարբերակում են մաքուր մաթեմատիկան և կիրառական մաթեմատիկան։ Այնուամենայնիվ, մաքուր մաթեմատիկայի թեմաները հաճախ կիրառություններ են ունենում, օրինակ թվերի տեսությունը կրիպտոգրաֆիայում։ Այս կարևոր փաստը, որ նույնիսկ «մաքրագույն» մաթեմատիկան հաճախ գործնական կիրառություն է ունենում, այն է, որ Յուջին Վիգները անվանել էր «Մաթեմատիկայի անտրամաբանական արդյունավետություն»"[30]։ Ինչպես հետազոտությունների բոլոր ոլորտներում, գիտելիքի պայթյունը գիտության դարում հանգեցրեց մասնագիտացման՝ այժմ մաթեմատիկայում հաշվվում են հարյուրավոր մասնագիտական բնագավառներ և վերջին մաթեմատիկական առարկայական դասակարգումը 46 էջ է զբաղեցնում[31]։ Կիրառական մաթեմատիկայի որոշ բնագավառներ միաձուլվել են արտաքին համապատասխան ավանդույթների հետ և դարձել են ինքնուրույն գիտության ճյուղ, ներառյալ վիճակագրությունը, գործողությունների հետազոտությունը և կոմպյուտերային գիտություն։
Մաթեմատիկայով զբաղվածների համար մաթեմատիկան որոշակի գեղագիտական գրավչություն ունի։ Շատ մաթեմատիկոսներ խոսում են մաթեմատիկայի էլեգանտության, ներքին էսթետիկայի և ներքին գեղեցկության մասին։ Պարզությունն ու ընդհանրությունը գնահատվում են։ Պարզ և էլեգանտ մաթեմատիկական ապացույցում, ինչպիսին Էվկլիդեսի պարզ թվերի անվերջ լինելու ապացույցը և Ֆուրյեի արագ ձևափոխության էլեգանտ հաշվարկային մեթոդը, որ արագացնում է հաշվարկը, գեղեցկություն կա։ Գոդֆրի Հարոլդ Հարդին իր Մաթեմատիկոսի ներողությունը գրքում այն համոզմունքն է արտահայտում, որ այս էսթետիկական նկատառումները բավարար են մաքուր մաթեմատիկան ուսումնասիրության հիմնավորման համար։ Նա մաթեմատիկական էսթետիկային նպաստող չափանիշներ սահմանեց՝ նշանակալիություն, անսպասելիություն, անխուսափելիություն և տնտեսություն[32]։ Մաթեմատիկոսները հաճախ ձգտում են գտնել հատկապես էլեգանտ ապացույցներ[33][34]։ Զվարճալի մաթեմատիկայի հանրայնությունը ևս մի ապացույց է, որ մաթեմատիկակական խնդիրներ լուծելը հաճելի զբաղմունք է։
Նշագրում, լեզու և խստություն

Այսօր օգտագործվող մաթեմատիկական նշագրումների մեծ մասը մինչ 16-րդ դարը դեռևս հայտնագործված չէր[35]։ Մինչ այդ, մաթեմատիկան գրված էր բառերով, ինչը սահմանափակում էր մաթեմատիկական հայտնագործությունը[36]։ Այսօր օգտագործվող նշագրումներից մեծ մասը Լեոնարդ Էյլերի (1707–1783) ստեղծածն է։ Ժամանակակից նշագրումները մասնագետների համար մաթեմատիկան դարձնում են ավելի հեշտացված, բայց սկսնակները վհատվում են դրանց տեսքից։ Ըստ Բարբարա Օուկլեյի՝ սա կարելի է բացատրել մաթեմատիկական գաղափարների աբստրակտ և ավելի կոդավորված լինելով[37]։ Ի տարբերություն բնական լեզվի, որտեղ մարդիկ կարող են բառին (օրինակ՝ կով) համապատասխան ֆիզիկական օբյեկտ հավասարեցնել, մաթեմատիկական սիմվոլները աբստրակտ են, չունեն որևէ ֆիզիկական անալոգ[38]։ Մաթեմատիկական սիմվոլներն ավելի խիստ են կոդավորված, քան սովորական բառերը, այսինքն՝ մեկ սիմվոլը կարող է կոդավորել տարբեր գործողություններ կամ գաղափարներ[39]։
Մաթեմատիկական լեզուն սկսնակների համար կարող է դժվար հասկանալի լինել, քանի որ նույնիսկ սովորական տերմիններն ինչպիսիք կամ և միակ, ունեն ավելի ճշգրիտ իմաստ, քան ամենօրյա խոսքում և այլ բաց և դաշտ տերմինները վերաբերում են հատուկ մաթեմատիկական գաղափարների։ Մաթեմատիկական լեզուն ներառում է նաև շատ տերմիններ, ինչպիսիք հոմոմորֆիզմն ու ինտեգրալը, որոնք մաթեմատիկայից դուրս իմաստ չունեն։ Մաթեմատիկան ավելի ճշգրտություն է պահանջում, քան ամենօրյա խոսքը։ Այդ է պատճառը, որ մաթեմատիկան հատուկ նշագրում և տեխնիկական բառապաշար ունի։ Մաթեմատիկոսները լեզվի ճշգրտությանն ու տրամաբանությանը վորաբերում են որպես "խստության".
Մաթեմատիկական ապացույցը հիմնականում խստության հարց է։ Մաթեմատիկոսները ցանկանում են, որ իրենց թեորեմները հետևեն աքսիոմներից համակարգված փաստարկների միջոցով։ Սպասվելիք խստության մակարդակը մաթեմատիկայում ժամանակի ընթացքում փոփոխվել է։ Հույները մանրամասն փաստարկներ էին պահանջում, սակայն Իսահակ Նյուտոնի ժամանակ կիրառվող մեթոդներն ավելի թույլ էին։ Նյուտոնի կողմից օգտագործվող սահմանումներում ծառացած խնդիրները 19-րդ դարում հանգեցրին մանրակրկիտ ուսումնասիրության և ֆորմալ ապացույցի վերափոխման։ Մաթեմատիկայի մի քանի ընդհանուր սխալների պատճառը խստության հասկացության սխալ ընկալումն է։ Այսօր մաթեմատիկոսները շարունակում են վիճել կոմպյուտերային ապացույցների վերաբերյալ։ Քանի որ խոշոր հաշվարկները դժվար է ստուգել, այդպիսի ապացույցները դժվար է ստուգել, այդպիսի ապացույցները չեն կարող խիստ լինել[40]։
Աքսիոմի ավանդական իմաստն էր՝ «ինքնին ակնհայտ ճշմարտություն», բայց այն խնդրահարույց է[41]։ Ֆորմալ մակարդակում աքսիոմը պարզապես սիմվոլների տող է, որը ներքին իմաստ ունի միայն աքսիոմատիկ համակարգից դուրս բերվող բոլոր բանաձևերի համատեքստում։ Հիլբերտի ծրագիրը նպատակ էր դրել մաթեմատիկան ամբողջությամբ դնել աքսիոմատիկ բազիսի վրա, սակայն Գյոդելի ոչ լրիվության թեորեմի համաձայն, յուրաքանչյուր (բավականաչափ հզոր) աքսիոմատիկ համակարգ անլուծելի բանաձևեր; ուստի մաթեմատիկայի վերջնական աքսիոմատիզացումն անհնար է։ Այնուամենայնիվ մաթեմատիկան հաճախ պատկերացնում են որպես որոշակի աքսիոմատիզացմամբ բազմությունների տեսություն, այն իմաստով, որ յուրաքանչյուր մաթեմատիկական պնդում կամ ապացույց կարելի է ներկայացնել բազմությունների տեսության բանաձևի միջոցով[42]։
Մաթեմատիկայի բաժիններ

Մաթեմատիկան լայն իմաստով կարող է բաժանվել մասերի, որոնք ուսումնասիրում են քանակը, կառուցվածքը, տարածությունը և փոփոխությունը (այսինքն թվաբանություն, հանրահաշիվ, երկրաչափություն, և մաթեմատիկական անալիզ)։ Բացի այս գլխավոր պրոբլեմների, գոյություն ունեն նաև ենթաուղղություններ, որ մաթեմատիկայից տանում են դեպի այլ բնագավառների՝ մաթեմատիկական տրամաբանություն, բազմությունների տեսություն (մաթեմատիկայի հիմունքներ), տարբեր գիտությունների փորձարարական մաթեմատիկա (կիրառական մաթեմատիկա), իսկ վերջերս անորոշություն մանրակրկիտ ուսումնասիրության։ Չնայած որոշ բնագավառներ կարող են կապակցված չթվալ, սակայն Լանգլանդս ծրագիրը գտել է նախկինում կապ չունեցող թվացող բաժինների, ինչպիսիք Գալուայի խմբեր, Ռիմանի մակերևույթի և թվերի տեսություն բաժինների միջև կապեր է հայտնաբերել։
Հիմունքներ և փիլիսոփայություն
Մաթեմատիկայի հիմունքները հստակեցնելու համար մշակվել են մաթեմատիկական տրամաբանություն և բազմությունների տեսություն ճյուղերը։ Մաթեմատիկական տրամաբանությունը ներառում է տրամաբանության մաթեմատիկական ուսումնասիրությունը և ձևական տրամաբանության կիրառումը մաթեմատիկայի այլ բնագավառներում; բազմությունների տեսությունը մաթեմատիկայի ճյուղ է, որ բազմություններ կամ օբյեկտների հավաքածուներ է ուսումնասիրում։ Կատեգորիաների տեսությունը, որ աբստրակտ մոտեցմամբ զբաղվում է մաթեմատիկական կառուցվածքներով և դրանց միջև եղած կապերով, դեռևս զարգացման փուլում է։ «Հիմունքների ճգնաժամը» արտահայտությունը նկարագրում է մոտավորապես 1900–1930 թվականներին տեղի ունեցած մաթեմատիկայի խիստ հիմքերի փնտրտուկը[43]։ Մաթեմատիկայի հիմունքների վերաբերյալ որոշ անհամաձայնություններ շարունակում են մնալ նաև այսօր։ Հիմունքների ճգնաժամը ժամանակին առաջացել է մի շարք հակասությունների պատճառով, ներառյալ Կանտորի տեսության և Բրաուեր-Հիլբերտի հակասությունները։
Մաթեմատիկական տրամաբանությունը մաթեմատիկան դնում է խիստ աքսիոմատիկ շրջանակում և ուսումնասիրում հետևանքները։ Այն Գյոդելի ոչ լրիվության թեորեմի միջավայրն է, որը (ոչ ֆորմալ) ենթադրում է, որ ցանկացած արդյունավետ ֆորմալ համակարգ, որում հիմնական թվաբանությունն առկա է, եթե ճիշտ են (այսինքն, բոլոր թեորեմները, որ կարելի է ապացուցել, ճիշտ են), անպայման լրիվ չեն (այսինքն, կան ճիշտ թեորեմներ, որոնք հնարավոր չի ապացուցել այդ համակարգում)։ Գյոդելը ցույց է տվել, որ ինչպիսին էլ լինի որպես հիմք վերցրած թվային-տեսական աքսիոմաների հավաքածուն, կարելի է կառուցել ճիշտ թվային-տեսական փաստերի ֆորմալ պնդում, որը հնարավոր չի դուրս բերել տրված աքսիոմներից։ Հետևաբար, ոչ մի ֆորմալ համակարգ չի կարող լիովին աքսիոմատիզացնել թվերի տեսությունը։ Ժամանակակից տրամաբանությունը բաղկացած է հաշվարկելիության տեսություն, մոդելների տեսություն, ապացույցների տեսություն կատեգորիաների տեսություն բաժիններից։
Տեսական ինֆորմատիկան ներառում է հաշվարկելիության տեսությունը, բարդությունների տեսությունը, և ինֆորմացիոն տեսությունը։ Հաշվարկելիության տեսությունը ուսումնասիրում է կոմպյուտերների տարբեր տեսական մոդելների, այդ թվում ամենահայտնի մոդելի՝ Թյուրինգի մեքենաների սահմանափակումները։ Բարդությունների տեսությունը ուսումնասիրում է կոմպյուտերի վրա խնդիրների լուծման ծախսատարությունը, որոշ պրոբլեմների լուծումն այնքան ժամանակ և հիշողություն են պահանջում, որ իրականում նրանց լուծումը կարող է անիրականալի լինել։ Այդպիսի պրոբլեմներից ամենահայտնին "P = NP հատընտիրի պրոբլեմն" է Հազարամյակի մրցանակային խնդիրների ցանկից[44]։ Ի վերջո, Ինֆորմացիոն տեսությունը գործ ունի տվյալների քանակի հետ, որը կարող է պահվել տվյալ կրիչի վրա, և հետևաբար գործ ունի տվյալների սեղմում և էնտրոպիա հասկացությունների հետ։



Մաթեմատիկական տրամաբանություն Բազմությունների տեսություն Կատեգորիաների տեսություն Ալգորիթմների տեսություն
Մաքուր մաթեմատիկա
Քանակ
Քանակի ուսումնասիրությունը սկսվում է թվերով, սկզբում ծանոթություն բնական թվերի և ամբողջ թվերի և դրանց նկատմամբ գործողությունների, որոնք նկարագրվում են թվաբանությունում։ Ամբողջ թվերի ավելի խորը հատկանիշներն ուսումնասիրվում են թվերի տեսության մեջ, որից հայտնի արդյունք կարելի է նշել Ֆերմայի մեծ թեորեմը։երկվորյակների հիպոթեզը և Գոլդբախի հիպոթեզը երկու չլուծված խնդիրներ են թվերի տեսությունում։
Թվային համակարգի զարգացմանը զուգահեռ թվերը ճանաչվեցին որպես ռացիոնալ թվերի ենթաբազմություն ("Կոտորակներ")։ Դրանք, իրենց հերթին, ընդգրկված են իրական թվերի մեջ, որոնք օգտագործվում են անընդհատ մեծություններ ներկայացնելու համար։ Իրական թվերը ընդհանրացվել են կոմպլեքս թվերի։ Սրանք թվերի հիերարխիայի առաջին քայլերն են, որոնք շարունակում են ներառել քվատերնիոններ և օկտոնիոններ։ Բնական թվերի դիտարկումը նույնպես հանգեցնում է տրանսֆինիտ թվերի, որոնք ձևավորում են «անսահմանություն» հասկացությունը։ Համաձայն հանրահաշվի հիմնական թեորեմի մեկ անհայտով կոմպլեքս գործակիցներով հավասարումների բոլոր լուծումները կոմպլեքս թվեր են, անկախ աստիճանից։ Ուսումնասիրության մեկ այլ բնագավառ բազմությունների չափն է, որը նկարագրվում է կարդինալ թվով։ Սրանց մեջ են մտնում ալեֆ թվերը, որոնք հնարավորություն են տալիս անվերջ մեծ բազմությունների չափերի իմաստալից համեմատություն։
Կառուցվածք
Շատ մաթեմատիկական օբյեկտներ, ինչպիսիք թվերի և ֆունկցիաների բազմություններն են, որպես գործողությունների կամ բազմության վրա սահմանված հարաբերությունների արդյունք ներքին կառուցվածք են դրսևորում։ Այնուհետ մաթեմատիկան ուսումնասիրում է այդ բազմությունների հատկությունները, որոնք կարող են արտահայտվել այդ կառուցվածքի տերմիններով; օրինակ, թվերի տեսությունը ուսումնասիրում է ամբողջ թվերի բազմության այն հատկությունները, որ կարող են արտահայտվել թվաբանական գործողություններով։ Ավելին, հաճախ է պատահում, որ տարբեր այդպիսի կառուցվածք ունեցող բազմություններ նմանատիպ հատկություններ են դրսևորում, որը հնարավորություն է ստեղծում աբստրակցիայի հաջորդ քայլում կառուցվածքների դասի համար աքսիոմներ ամրագրել և այնուհետ ուսումնասիրել այդ աքսիոմներին բավարարող կառուցվածքների ողջ դասը։ Այսպիսով կարելի է ուսումնասիրել խմբեր, օղակներ, դաշտեր և այլ աբստրակտ համակարգեր; այսպիսի համատեղ ուսումնասիրությունները (հանրահաշվական գործողություններով սահմանված կառուցվածքների համար) կազմում են աբստրակտ հանրահաշվի տիրույթը։
Իր լայն ընդհանրությամբ աբստրակտ հանրահաշիվը հաճախ կարող է կիրառվել առերևույթ կապ չունեցող խնդիրների նկատմամբ; քանոնի և կարկինի օգնությամբ կառուցողական հնագույն խնդիրների մեծ մասը վերջնականապես լուծում ստացան օգտվելով Գալուայի թեորեմից, որը ներառում է դաշտերի տեսությունը և խմբերի տեսությունը։ Հանրահաշվի տեսության մեկ այլ օրինակ է գծային հանրահաշիվը, որը վեկտորական տարածության ընդհանուր ուսումնասիրությունն է։ Վեկտորական տարածության տարրերը կոչվում են վեկտորներ, որոնք ունեն քանակ և ուղղություն և կարող են օգտագործվել տարածության մեջ կետերի միջև հարաբերությունները մոդելավորելու համար։ Սա մի օրինակ է նախնական ոչ կապակցված բնագավառներ՝ երկրաչափությունը և հանրահաշիվը, ժամանակակից մաթեմատիկայում խիստ փոխկապակցված են։ Կոմբինատորիկան ուսումնասիրում է տվյալ կառուցվածքին համապատասխան օբյեկտների քանակի թվարկման ուղիները։




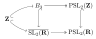
Կոմբինատորիկա Թվերի տեսություն Խմբերի տեսություն Գրաֆների տեսություն Կարգավորման տեսություն Հանրահաշիվ
Տարածություն
Տիեզերքի ուսումնասիրությունը սկսվում է երկրաչափությունից – մասնավորապես Էվկլիդեսյան երկրաչափությունից, որը միավորում է տարածությունն ու թվերը և ներառում է հայտնի Պյութագորասի թեորեմը։
Եռանկյունաչափությունը մաթեմատիկայի ճյուղ է, որը եռանկյունաչափական ֆունկցիաների միջոցով ուսումնասիրում է եռանկյան կողմերի և անկյունների հարաբերությունները։ Տարածության ժամանակակից ուսումնասիրություններն ընդհանրացնում են այս գաղափարները ներառելու բարձր-չափանի երկրաչափությունը՝ ոչ-Էվկլիդեսյան երկրաչափություն և տոպոլոգիա։ Քանակը և տարածությունը դեր ունեն անալիտիկ երկրաչափության, դիֆերենցիալ երկրաչափության և հանրահաշվական երկրաչափությունում։ Ուռուցիկ երկրաչափություն|Ուռուցիկ և դիսկրետ երկրաչափությունը մշակվել են թվերի երկրաչափության և ֆունկցիոնալ անալիզի խնդիրները լուծելու համար, սակայն այժմ դիտարկվում են օպտիմիզացիայի և ինֆորմատիկայի կիրառություններում։ Դիֆերենցիալ երկրաչափության մեջ ուսումնասիրում է շերտավորում հասկացողություն և բազմաձևությունների հաշիվ, մասնավորապես, վեկտորային և տենզորային հաշիվ։ Հանրահաշվական երկրաչափությունում երկրաչափական օբյեկտները ներկայացվում են որպես բազմանդամային հավասարումների լուծումների բազմություն, որտեղ զուգակցում են քանակի և տարածության հասկացությունները, և միաժամանակ տոպոլոգիական խմբերի ուսումնասիրությունը, որոնք միավորում են կառուցվածքն ու տարածությունը։ Լի խմբերը օգտագործվում են ուսումնասիրելու տարածությունը, կառուցվածքը և փոփոխությունները։ Տոպոլոգիան իր բոլոր բազմաթիվ դրսևորումներով 20-րդ դարի մաթեմատիկայում ամենամեծ աճն է ունեցել, այն ներառում է ընդհանուր տոպոլոգիան, բազմությունների ընդհանուր տոպոլոգիան, հանրահաշվական տոպոլոգիան և դիֆերենցիալ տոպոլոգիան։ Մասնավորապես, ժամանակակից տոպոլոգիայի օրինակներ են՝ մետրիկական տեսություն, բազմությունների աքսիոմատիկ տեսություն, Հոմոտոպիա և Մորսի տեսություն։ Տոպոլոգիան նաև ներառում է այժմ լուծված Պուանկարեի հիպոթեզը և դեռևս չլուծված Հոջի հիպոթեզը։ Երկրաչափության և տոպոլոգիայի այլ արդյունքներ, ներառյալ չորս գույների թեորեմը և Կեպլերի հիպոթեզը, ապացուցվել են միայն կոմպյուտերի օգնությամբ։






Երկրաչափություն Եռանկյունաչափություն Դիֆերենցիալ երկրաչափություն Տոպոլոգիա Ֆրակտալ երկրաչափություն Չափերի տեսություն
Փոփոխություն
Փոփոխությունների ըմբռնումն ու նկարագրությունը Understanding and describing change is a common theme in the բնական գիտությունների ընդհանուր թեման է, իսկ մաթեմատիկական անալիզը մշակվել է դրանք ուսումնասիրելու համար որպես հզոր գործիք։ Ֆունկցիան այստեղ առաջացել է որպես քանակի փոփոխության կենտրոնական հասկացություն։ Իրական թվերի և իրական փոփոխականների ֆունկցիաների խորը ուսումնասիրությունը հայտնի է որպես իրական անալիզ, իսկ կոմպլեքս թվերի դաշտինը՝ համապատասխանաբար, որպես կոմպլեքս անալիզ։ Ֆունկցիոնալ անալիզը կենտրոնանում է (հիմնականում անվերջ-չափանի) ֆունկցիաների տարածության վրա։ Ֆունկցիոնալ անալիզի բազմաթիվ կիրառություններից է քվանտային մեխանիկան։ Բազմաթիվ պրոբլեմներ կապված են քանակի և դրա փոփոխության արագությամբ և դրանք ուսումնասիրվում են որպես դիֆերենցիալ հավասարումներ։ Բնության բազմաթիվ երևույթներ կարող են ներկայացվել դինամիկ համակարգերի, քաոսային տեսության միջոցով, որը թույլ է տալիս ճշգրիտ որոշել, որ այս համակարգերից շատերը ցուցաբերում են դեռևս անկանխատեսելի դետերմինացված վարքագիծ։
 |
 |
 |
 |
 |

|
| Հաշիվ | Վեկտորական հաշիվ | Դիֆերենցիալ հավասարումներ | Դինամիկ համակարգեր | Քաոսային տեսություն | Կոմպլեքս անալիզ |
Կիրառական մաթեմատիկա
Կիրառական մաթեմատիկան վերաբերում է գիտության, ճարտարագիտության, բիզնեսի և արդյունաբերության մեջ սովորաբար օգտագործվող մաթեմատիկական մեթոդներին։ Այսպիսով, "կիրառական մաթեմատիկան" մասնագիտացված գիտելիքներով մաթեմատիկական գիտություն է։ Կիրառական մաթեմատիկա տերմինը նաև նկարագրում է մասնագիտական ուղղվածությունը, որտեղ մաթեմատիկոսներն աշխատում են պրակտիկ պրոբլեմների վրա, որպես պրակտիկ պրոբլեմների վրա կենտրոնացած մասնագիտություն կիրառական մաթեմատիկան զբաղվում է գիտության, ճարտարագիտության և մաթեմատիկական պրակտիկայի տարբեր ճյուղերի "մաթեմատիկական մոդելների ձևակերպմամբ, ուսումնասիրությամբ և օգտագործմամբ։
Անցյալում պրակտիկ կիրառություններն են նպաստել մաթեմատիկական տեսությունների զարգացմանը, որոնք հետագայում դառնում էին մաքուր մաթեմատիկայի ուսումնասիրության առարկա, որտեղ մաթեմատիկան զարգանում է հիմնականում իր համար։ Այսպիսով կիրառական մաթեմատիկան կենսականորեն կապված է մաքուր մաթեմատիկայի հետազոտությունների հետ։
Վիճակագրություն և որոշումների կայացման այլ գիտություններ
Կիրառական մաթեմատիկան նշանակալիորեն հատվում է վիճակագրության ուղղության, հատկապես հավանականությունների տեսության, հետ, որի տեսությունը մաթեմատիկորեն ձևակերպված է։ Վիճակագրողները (աշխատելով որպես հետազոտական նախագծի հատված) պատահական ընտրության և պատահական փորձերի մշակման հետ "ստեղծում են տվյալներ, որ իմաստ ունեն";[45] վիճակագրական ընտրության կամ փորձի մշակումը որոշում է տվյալների վերլուծությունը (մինչ տվյալները հասանելի լինելը)։ Փորձարկումների և օրինակների տվյալները վերանայելիս կամ դիտարկումների տվյալները վերլուծելիս, վիճակագիրները, օգտագործելով վիճակագրական մոդելավորումը և հետևությունների տեսությունը, մոդելի ընտրությամբ և գնահատմամբ, "տվյալներին իմաստ են տալիս"։ Վիճակագրությունը ավելի շուտ առանձին ուղղություն է, քան կիրառական մաթեմատիկայի ճյուղ։ Հետազոտող ֆիզիկոսների ու ինֆորմատիկայով զբաղվող գիտնականների նման հետազոտող վիճակագիրները մաթեմատիկոս գիտնականներ են։ Շատ վիճակագիրներ ունեն մաթեմատիկայի աստիճաններ և որոշ վիճակագիրներ նաև մաթեմատիկոսներ են։
Հաշվողական մաթեմատիկա
Հաշվողական մաթեմատիկան մաթեմատիկական պրոբլեմների լուծման համար առաջարկում և ուսումնասիրում է այնպիսի մեթոդներ, որոնք սովորաբար չափազանց մեծ են մարդկային թվային ունակության համար։ Թվային անալիզը ուսումնասիրում է մաթեմատիկական անալիզի պրոբլեմները օգտագործելով ֆունկցիոնալ անալիզ և մոտարկումների տեսություն; թվային անալիզը ներառում է մոտարկումների ուսումնասիրությունը և լայն իմաստով դիսկրետիզացումը, հատուկ ուշադրություն դարձնելով մոտարկման սխալների վրա։ Թվային անալիզը և ավելի լայն գիտական հաշվարկները ուսումնասիրում են նաև մաթեմատիկական գիտության ոչ անալիտիկ թեմաները, հատկապես ալգորիթմական մատրիցային և գրաֆների տեսությունը։
 |
 |
 |
 |
 |
||
| Խաղերի տեսություն | Հեղուկի դինամիկա | Թվային մեթոդներ | Մաթեմատիկական օպտիմիզացում | Հավանականությունների տեսություն | Վիճակագրություն | Կրիպտոգրաֆիա |
 |
 |
 |
 |
|||
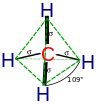
| Ֆինանսների մաթեմատիկա | Մաթեմատիկական ֆիզիկա | Մաթեմատիկական քիմիա | Մաթեմատիկական կենսաբանություն | Մաթեմատիկական տնտեսագիտություն | Կառավարման տեսություն |
Մաթեմատիկական մրցանակներ
Մաթեմատիկայի ամենահեղինակավոր մրցանակը Ֆիլդսյան մրցանակն է,[46][47] որ հիմնադրվել է 1936 թվականին և տրվում է չորս տարին մեկ (բացի II համաշխարհային պատերազմի տարիներին) ամենաշատը չորս անհատի։ Ֆիելդսյան մեդալը հաճախ դիտարկվում է Նոբելյան մրցանակի մաթեմատիկական էկվիվալենտ։
Մաթեմատիկայի Վոլֆի մրցանակը, հիմնված 1978 թվականին, ճանաչում է ձեռքբերումները կենդանության օրոք, և մեկ այլ միջազգային մրցանակ՝ Աբելի մրցանակը հիմնվել է 2003 թվականին։ Չերնի մրցանակը հիմնվել է 2010 թվականին կենդանության օրոք հաջողությունները ճանաչելու համար։ Այս մրցանակները տրվում են կոնկրետ նորարարական աշխատանքի կամ կոնկրետ բնագավառում չլուծված հայտնի խնդրի լուծման համար։
23 հայտնի բաց պրոբլեմների ցանկը, որ կոչվում է «Հիլբերտի պրոբլեմներ», կազմվել է 1900 թվականին գերմանացի մաթեմատիկոս Դավիդ Հիլբերտի կողմից։ Այս ցուցակը մաթեմատիկոսների շրջանում մեծ հեղինակություն է վայելում և դրանցից այժմ արդեն լուծված են։ 2000 թվականին հրապարակվել է յոթ կարևորագույն պրոբլեմների՝ «Հազարամյակի մրցանակային խնդիրներ»" նոր ցուցակը։ Յուրաքանչյուր պրոբլեմի լուծման համար նախատեսված է 1 միլիոն դոլարի մրցանակ, որոնցից միայն մեկն է (Ռիմանի հիպոթեզը) կրկնվում Հիլբերտի պրոբլեմների մեջ։
Տես նաև
- Մաթեմատիկայի պատմությունը
- Մաթեմատիկայի փիլիսոփայություն
- Մաթեմատիկական թեմաների ցանկ
- Մաթեմատիկա և արվեստ
- Տարրական մաթեմատիկա
- Մաթեմատիկայի ազգային թանգարան
- Մաթեմատիկայի և ֆիզիկայի կապը
- Գիտություն, Տեխնիկա, Ճարտարագիտություն և Մաթեմատիկա
Նշումներ
Ծանոթագրություններ
- ↑ «Ժամանակակից հայոց լեզվի բացատրական բառարան, Հրաչյա Աճառյանի Անվան Լեզվի Ինստիտուտ - ուսողություն». www.nayiri.com. Վերցված է 2024 թ․ հունիսի 16-ին.
- ↑ «mathematics | Definition & History». Encyclopedia Britannica (անգլերեն). Վերցված է 2018 թ․ նոյեմբերի 19-ին.
- ↑ «Webster's Online Dictionary». Արխիվացված է օրիգինալից 2013 թ․ հոկտեմբերի 29-ին. Վերցված է 2013 թ․ հունվարի 5-ին.
- ↑ Eves, p. 306
- ↑ Marcus du Sautoy, A Brief History of Mathematics: 1. Newton and Leibniz Արխիվացված Դեկտեմբեր 6, 2012 Wayback Machine, BBC Radio 4, September 27, 2010.
- ↑ 6,0 6,1 Waltershausen, p. 79
- ↑ Peirce, p. 97.
- ↑ Hilbert, D. (1919–20), Natur und Mathematisches Erkennen: Vorlesungen, gehalten 1919–1920 in Göttingen. Nach der Ausarbeitung von Paul Bernays (Edited and with an English introduction by David E. Rowe), p. 14, Basel, Birkhäuser (1992).
- ↑ 9,0 9,1 Einstein, p. 28. The quote is Einstein's answer to the question: "How can it be that mathematics, being after all a product of human thought which is independent of experience, is so admirably appropriate to the objects of reality?" This question was inspired by Eugene Wigner's paper "The Unreasonable Effectiveness of Mathematics in the Natural Sciences".
- ↑ Peterson, p. 12
- ↑ Dehaene, Stanislas; Dehaene-Lambertz, Ghislaine; Cohen, Laurent (1998 թ․ օգոստոս). «Abstract representations of numbers in the animal and human brain». Trends in Neurosciences. 21 (8): 355–61. doi:10.1016/S0166-2236(98)01263-6. ISSN 0166-2236. PMID 9720604.
- ↑ See, for example, Raymond L. Wilder, Evolution of Mathematical Concepts; an Elementary Study, passim
- ↑ Kline 1990, Chapter 1.
- ↑ "A History of Greek Mathematics: From Thales to Euclid Արխիվացված Հունվար 8, 2014 Wayback Machine". Thomas Little Heath (1981). 0-486-24073-8
- ↑ Sevryuk, 2006, էջեր 101–09
- ↑ «mathematic». Online Etymology Dictionary. Արխիվացված օրիգինալից 2013 թ․ մարտի 7-ին.
- ↑ Both senses can be found in Plato. Կաղապար:LSJ
- ↑ Boas, Ralph (1995) [1991]. «What Augustine Didn't Say About Mathematicians». Lion Hunting and Other Mathematical Pursuits: A Collection of Mathematics, Verse, and Stories by the Late Ralph P. Boas, Jr. Cambridge University Press. էջ 257.
- ↑ James Franklin, "Aristotelian Realism" in Philosophy of Mathematics, ed. A.D. Irvine, p. 104 Արխիվացված Սեպտեմբեր 6, 2015 Wayback Machine. Elsevier (2009).
- ↑ Cajori, Florian (1893). A History of Mathematics. American Mathematical Society (1991 reprint). էջեր 285–86. ISBN 0-8218-2102-4.
- ↑ 21,0 21,1 21,2 Mura, Roberta (1993 թ․ դեկտեմբեր). «Images of Mathematics Held by University Teachers of Mathematical Sciences». Educational Studies in Mathematics. 25 (4): 375–385. doi:10.1007/BF01273907. JSTOR 3482762.
- ↑ Tobies, Renate; Helmut Neunzert (2012). Iris Runge: A Life at the Crossroads of Mathematics, Science, and Industry. Springer. էջ 9. ISBN 3-0348-0229-3. «[I]t is first necessary to ask what is meant by mathematics in general. Illustrious scholars have debated this matter until they were blue in the face, and yet no consensus has been reached about whether mathematics is a natural science, a branch of the humanities, or an art form.»
{cite book}: Invalid|name-list-style=yes(օգնություն) - ↑ 23,0 23,1 23,2 Snapper, Ernst (1979 թ․ սեպտեմբեր). «The Three Crises in Mathematics: Logicism, Intuitionism, and Formalism». Mathematics Magazine. 52 (4): 207–16. doi:10.2307/2689412. JSTOR 2689412.
{cite journal}: CS1 սպաս․ postscript (link) - ↑ Peirce, Benjamin (1882). Linear Associative Algebra. էջ 1. Արխիվացված օրիգինալից 2015 թ․ սեպտեմբերի 6-ին.
- ↑ Bertrand Russell, The Principles of Mathematics, p. 5 Արխիվացված Սեպտեմբեր 6, 2015 Wayback Machine. University Press, Cambridge (1903)
- ↑ Curry, Haskell (1951). Outlines of a Formalist Philosophy of Mathematics. Elsevier. էջ 56. ISBN 0-444-53368-0.
- ↑ du Sautoy, Marcus (2010 թ․ հունիսի 25). «Nicolas Bourbaki». A Brief History of Mathematics. Event occurs at min. 12:50. BBC Radio 4. Արխիվացված օրիգինալից 2016 թ․ դեկտեմբերի 16-ին. Վերցված է 2017 թ․ հոկտեմբերի 26-ին.
- ↑ Shasha, Dennis Elliot; Lazere, Cathy A. (1998). Out of Their Minds: The Lives and Discoveries of 15 Great Computer Scientists. Springer. էջ 228.
- ↑ Popper 1995, p. 56
- ↑ Wigner, Eugene (1960). «The Unreasonable Effectiveness of Mathematics in the Natural Sciences». Communications on Pure and Applied Mathematics. 13 (1): 1–14. Bibcode:1960CPAM...13....1W. doi:10.1002/cpa.3160130102. Արխիվացված է օրիգինալից 2011 թ․ փետրվարի 28-ին. Վերցված է 2018 թ․ փետրվարի 3-ին.
- ↑ «Mathematics Subject Classification 2010» (PDF). Արխիվացված (PDF) օրիգինալից 2011 թ․ մայիսի 14-ին. Վերցված է 2010 թ․ նոյեմբերի 9-ին.
- ↑ Hardy, G.H. (1940). A Mathematician's Apology. Cambridge University Press. ISBN 0-521-42706-1.
- ↑ Gold, Bonnie; Simons, Rogers A. (2008). Proof and Other Dilemmas: Mathematics and Philosophy. MAA.
- ↑ Aigner, Martin; Ziegler, Günter M. (2001). Proofs from The Book. Springer. ISBN 3-540-40460-0.
- ↑ «Earliest Uses of Various Mathematical Symbols». Արխիվացված օրիգինալից 2016 թ․ փետրվարի 20-ին. Վերցված է 2014 թ․ սեպտեմբերի 14-ին.
- ↑ Kline, p. 140, on Diophantus; p. 261, on Vieta.
- ↑ Oakley 2014, p. 16: "Focused problem solving in math and science is often more effortful than focused-mode thinking involving language and people. This may be because humans haven't evolved over the millennia to manipulate mathematical ideas, which are frequently more abstractly encrypted than those of conventional language."
- ↑ Oakley 2014, p. 16: "What do I mean by abstractness? You can point to a real live cow chewing its cud in a pasture and equate it with the letters c–o–w on the page. But you can't point to a real live plus sign that the symbol '+' is modeled after – the idea underlying the plus sign is more abstract."
- ↑ Oakley 2014, p. 16: "By encryptedness, I mean that one symbol can stand for a number of different operations or ideas, just as the multiplication sign symbolizes repeated addition."
- ↑ Ivars Peterson, The Mathematical Tourist, Freeman, 1988, 0-7167-1953-3. p. 4 "A few complain that the computer program can't be verified properly", (in reference to the Haken–Apple proof of the Four Color Theorem).
- ↑ "The method of 'postulating' what we want has many advantages; they are the same as the advantages of theft over honest toil." Bertrand Russell (1919), Introduction to Mathematical Philosophy, New York and London, p. 71. Արխիվացված Հունիս 20, 2015 Wayback Machine
- ↑ Patrick Suppes, Axiomatic Set Theory, Dover, 1972, 0-486-61630-4. p. 1, "Among the many branches of modern mathematics set theory occupies a unique place: with a few rare exceptions the entities which are studied and analyzed in mathematics may be regarded as certain particular sets or classes of objects."
- ↑ Luke Howard Hodgkin & Luke Hodgkin, A History of Mathematics, Oxford University Press, 2005.
- ↑ Clay Mathematics Institute, P=NP, claymath.org
- ↑ Rao, C.R. (1997) Statistics and Truth: Putting Chance to Work, World Scientific. 981-02-3111-3
- ↑ Monastyrsky, 2001, էջ 1
- ↑ Riehm, 2002, էջեր 778–82

| Վիքիքաղվածքն ունի նյութեր, որոնք վերաբերում են «Մաթեմատիկա» հոդվածին։ |
| Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Մաթեմատիկա» հոդվածին։ |
| ||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||
| Այս հոդվածն ընտրվել է Հայերեն Վիքիպեդիայի՝ 2018 թվականի 47-րդ շաբաթվա հոդված։ |























