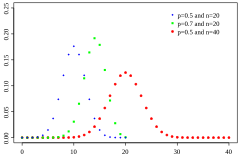
Rozkład dwumianowy

${\displaystyle n\geqslant 0}$ liczba prób (liczba całkowita)
${\displaystyle 0\leqslant p\leqslant 1}$ prawdopodobieństwo sukcesu (liczba rzeczywista)

${\displaystyle k\in \{0,\dots ,n\}$

${\displaystyle {n \choose k}p^{k}(1-p)^{n-k}$

${\displaystyle I_{1-p}(n-\lfloor k\rfloor ,1+\lfloor k\rfloor )}$

${\displaystyle np}$

jedna z ${\displaystyle \{\lfloor np\rfloor -1,{}$${\displaystyle \lfloor np\rfloor ,\lfloor np\rfloor +1\}$

${\displaystyle \lfloor (n+1)\,p\rfloor }$

${\displaystyle np(1-p)}$

${\displaystyle {\frac {1-2p}{\sqrt {np(1-p)}$

${\displaystyle {\frac {1-6p(1-p)}{np(1-p)}$

${\displaystyle {\frac {1}{2}\ln(2\pi nep(1-p))\,{}$${\displaystyle {}+O\left({\frac {1}{n}\right)}$

${\displaystyle (1-p+pe^{t})^{n}$

${\displaystyle (1-p+pe^{it})^{n}$

George Udny Yule (1911)