在概率论 和统计学 中,二项分布 (英語:binomial distribution )是一种离散 概率分布 ,描述在进行独立 随机试验 时,每次试验都有相同概率 “成功”的情况下,获得成功的总次数。掷硬币 十次出现五次正面的概率、产品合格率
99
%
{\displaystyle \,99\%\,}
只有“成功”和“失败”两种可能结果 ,每次重复时成功概率不变的独立随机试验称作伯努利试验 ,例如上述的掷硬币出现正面或反面、对产品进行抽样检查时抽到正品或次品。伯努利试验作为理论模型,其前提在现实中无法完全得到满足,比如生产线会磨损,因此每件产品合格的概率并非固定。尽管如此,二项分布给出的概率通常足以用于提供有用的推断;即使在已知前提没有满足的场合,二项分布也能用于参考和比较。二项分布的应用出现在遗传学 、质量控制 等领域之中。
若随机变量
X
{\displaystyle \,X\,}
概率质量函数
Pr
(
X
=
k
)
=
(
n
k
)
p
k
(
1
−
p
)
n
−
k
(
k
=
0
,
1
,
…
,
n
)
,
{\displaystyle \Pr(X=k)={n \choose k}p^{k}(1-p)^{n-k}\quad (k=0,1,\ldots ,n),}
其中
n
{\displaystyle \,n\,}
正整数 、
0
≤
p
≤
1
{\displaystyle \,0\leq p\leq 1\,}
X
{\displaystyle \,X\,}
参数 为
n
,
p
{\displaystyle \,n,p\,}
X
∼
B
(
n
,
p
)
{\displaystyle \,X\sim \operatorname {B} (n,p)\,}
X
∼
Bin
(
n
,
p
)
{\displaystyle \,X\sim \operatorname {Bin} (n,p)\,}
1
−
p
{\displaystyle \,1-p\,}
q
{\displaystyle \,q\,}
进行
n
{\displaystyle \,n\,}
独立 伯努利试验 的结果可以由
n
{\displaystyle \,n\,}
S
{\displaystyle \,S\,}
F
{\displaystyle \,F\,}
S
S
F
S
F
{\displaystyle SSFSF}
表示五次试验中第一、二、四次的结果为成功,其余为失败。设每次试验成功的概率为
p
{\displaystyle \,p\,}
1
−
p
{\displaystyle \,1-p\,}
k
{\displaystyle \,k\,}
S
{\displaystyle \,S\,}
n
−
k
{\displaystyle \,n-k\,}
F
{\displaystyle \,F\,}
p
k
(
1
−
p
)
n
−
k
{\displaystyle \,p^{k}(1-p)^{n-k}\,}
从
n
{\displaystyle \,n\,}
元素 中选出含
k
{\displaystyle \,k\,}
子集 的方法数量等于二项式系数
(
n
k
)
=
n
!
k
!
(
n
−
k
)
!
.
{\displaystyle {n \choose k}={\frac {n!}{k!(n-k)!}.}
而每种对
k
{\displaystyle \,k\,}
S
{\displaystyle \,S\,}
n
−
k
{\displaystyle \,n-k\,}
F
{\displaystyle \,F\,}
n
{\displaystyle \,n\,}
k
{\displaystyle \,k\,}
S
{\displaystyle \,S\,}
(
n
k
)
{\displaystyle \,{n \choose k}\,}
(
n
k
)
p
k
(
1
−
p
)
n
−
k
.
{\displaystyle {n \choose k}p^{k}(1-p)^{n-k}.}
二项分布是最早得到研究的概率分布之一。丹麦统计学家安德斯·哈爾德 认为其历史可以追溯至布莱兹·帕斯卡 与皮埃尔·德·费马 于1654年对点数分配问题 的讨论:两名玩家赢得每局游戏的机会相同,赢得一定局数的胜者可获得奖金,但比赛仅进行了数局,尚未分出胜负就被迫中断,则奖金该如何分配?帕斯卡认为,奖金的分配应当基于玩家距离胜利所差的局数:若一名玩家还需
r
{\displaystyle \,r\,}
s
{\displaystyle \,s\,}
r
+
s
−
1
{\displaystyle \,r+s-1\,}
2
r
+
s
−
1
{\displaystyle \,2^{r+s-1}\,}
p
=
1
/
2
{\displaystyle \,p=1/2\,}
对二项分布概率的推导为雅各布·伯努利 于《猜度术 概率论 的奠基性作品。伯努利还在其中首次给出了弱大数定律 的严格证明。对二项分布的正态 近似则是由亞伯拉罕·棣莫弗 发现,这一工作于1733年完成,于1738年出版在其著作《机遇论
参数为
n
,
p
{\displaystyle \,n,p\,}
期望值 为
n
p
{\displaystyle \,np\,}
方差 为
n
p
(
1
−
p
)
{\displaystyle \,np(1-p)\,}
概率母函数 为
G
(
z
)
=
(
1
−
p
+
p
z
)
n
,
{\displaystyle G(z)=(1-p+pz)^{n},}
矩母函数 为
M
X
(
t
)
=
(
1
−
p
+
p
e
t
)
n
,
{\displaystyle M_{X}(t)=(1-p+pe^{t})^{n},}
特征函数 为
φ
X
(
t
)
=
(
1
−
p
+
p
e
i
t
)
n
.
{\displaystyle \varphi _{X}(t)=(1-p+pe^{it})^{n}.}
参数
n
=
1
{\displaystyle \,n=1\,}
伯努利分布 。多项分布 超几何分布 的极限形式。
若
X
1
,
X
2
{\displaystyle \,X_{1},X_{2}\,}
n
1
,
p
{\displaystyle \,n_{1},p\,}
n
2
,
p
{\displaystyle \,n_{2},p\,}
X
1
+
X
2
{\displaystyle \,X_{1}+X_{2}\,}
n
1
+
n
2
{\displaystyle \,n_{1}+n_{2}\,}
X
1
+
X
2
{\displaystyle \,X_{1}+X_{2}\,}
n
1
+
n
2
,
p
{\displaystyle \,n_{1}+n_{2},p\,}
X
1
+
X
2
=
k
{\displaystyle \,X_{1}+X_{2}=k\,}
X
1
{\displaystyle \,X_{1}\,}
条件概率分布 是参数为
k
,
n
1
,
n
1
+
n
2
{\displaystyle \,k,n_{1},n_{1}+n_{2}\,}
计算
Pr
(
X
=
k
)
{\displaystyle \,\Pr(X=k)\,}
Pr
(
X
=
k
+
1
)
{\displaystyle \,\Pr(X=k+1)\,}
Pr
(
X
=
k
+
1
)
Pr
(
X
=
k
)
=
(
n
−
k
)
p
(
k
+
1
)
(
1
−
p
)
(
k
=
0
,
1
,
…
,
n
−
1
)
,
{\displaystyle {\frac {\Pr(X=k+1)}{\Pr(X=k)}={\frac {(n-k)p}{(k+1)(1-p)}\quad (k=0,1,\ldots ,n-1),}
因此,当
k
<
(
n
+
1
)
p
−
1
{\displaystyle \,k<(n+1)p-1\,}
Pr
(
X
=
k
)
{\displaystyle \,\Pr(X=k)\,}
k
{\displaystyle \,k\,}
k
>
(
n
+
1
)
p
−
1
{\displaystyle \,k>(n+1)p-1\,}
Pr
(
X
=
k
)
{\displaystyle \,\Pr(X=k)\,}
k
{\displaystyle \,k\,}
众数 为
(
n
+
1
)
p
{\displaystyle \,(n+1)p\,}
下取整
⌊
(
n
+
1
)
p
⌋
{\displaystyle \,\lfloor (n+1)p\rfloor \,}
(
n
+
1
)
p
{\displaystyle \,(n+1)p\,}
(
n
+
1
)
p
{\displaystyle \,(n+1)p\,}
(
n
+
1
)
p
−
1
{\displaystyle \,(n+1)p-1\,}
p
<
(
n
+
1
)
−
1
{\displaystyle \,p<(n+1)^{-1}\,}
0
{\displaystyle \,0\,}
二项分布的中位数
m
{\displaystyle \,m\,}
n
p
{\displaystyle \,np\,}
取整 之间,即
⌊
n
p
⌋
≤
m
≤
⌈
n
p
⌉
{\displaystyle \,\lfloor np\rfloor \leq m\leq \lceil np\rceil \,}
n
p
{\displaystyle \,np\,}
m
=
n
p
{\displaystyle \,m=np\,}
m
{\displaystyle \,m\,}
n
p
{\displaystyle \,np\,}
|
m
−
n
p
|
<
max
{
p
,
1
−
p
}
.
{\displaystyle |m-np|<\max\{p,1-p\}.}
若
p
>
ln
2
{\displaystyle \,p>\ln 2\,}
p
<
1
−
ln
2
{\displaystyle \,p<1-\ln 2\,}
|
m
−
n
p
|
<
ln
2.
{\displaystyle |m-np|<\ln 2.}
若
n
{\displaystyle \,n\,}
奇数 、
p
=
1
/
2
{\displaystyle \,p=1/2\,}
(
n
−
1
)
/
2
{\displaystyle \,(n-1)/2\,}
(
n
+
1
)
/
2
{\displaystyle \,(n+1)/2\,}
二项分布的累积分布函数 和尾概率可以用正则化不完全贝塔函数 表示为
Pr
(
X
≤
k
)
=
I
1
−
p
(
n
−
⌊
k
⌋
,
⌊
k
⌋
+
1
)
,
{\displaystyle \Pr(X\leq k)=I_{1-p}(n-\lfloor k\rfloor ,\lfloor k\rfloor +1),}
Pr
(
X
≥
k
)
=
I
p
(
⌈
k
⌉
,
n
−
⌈
k
⌉
+
1
)
.
{\displaystyle \Pr(X\geq k)=I_{p}(\lceil k\rceil ,n-\lceil k\rceil +1).}
二项分布的
r
{\displaystyle \,r\,}
原点矩 满足
μ
r
′
=
E
[
X
r
]
=
∑
j
=
0
r
S
(
r
,
j
)
n
!
p
j
(
n
−
j
)
!
,
{\displaystyle \mu '_{r}=E[X^{r}]=\sum _{j=0}^{r}{\frac {S(r,j)n!p^{j}{(n-j)!},}
其中
S
(
r
,
j
)
{\displaystyle \,S(r,j)\,}
第二类 斯特林数 。具体而言,
μ
1
′
=
n
p
,
{\displaystyle \mu '_{1}=np,}
μ
2
′
=
n
p
+
n
(
n
−
1
)
p
2
,
{\displaystyle \mu '_{2}=np+n(n-1)p^{2},}
μ
3
′
=
n
p
+
3
n
(
n
−
1
)
p
2
+
n
(
n
−
1
)
(
n
−
2
)
p
3
,
{\displaystyle \mu '_{3}=np+3n(n-1)p^{2}+n(n-1)(n-2)p^{3},}
μ
4
′
=
n
p
+
7
n
(
n
−
1
)
p
2
+
6
n
(
n
−
1
)
(
n
−
2
)
p
3
+
n
(
n
−
1
)
(
n
−
2
)
(
n
−
3
)
p
4
.
{\displaystyle \mu '_{4}=np+7n(n-1)p^{2}+6n(n-1)(n-2)p^{3}+n(n-1)(n-2)(n-3)p^{4}.}
其低阶中心矩 为
μ
2
=
n
p
(
1
−
p
)
,
{\displaystyle \mu _{2}=np(1-p),}
μ
3
=
n
p
(
1
−
p
)
(
1
−
2
p
)
,
{\displaystyle \mu _{3}=np(1-p)(1-2p),}
μ
4
=
3
[
n
p
(
1
−
p
)
]
2
+
n
p
(
1
−
p
)
[
1
−
6
p
(
1
−
p
)
]
.
{\displaystyle \mu _{4}=3[np(1-p)]^{2}+np(1-p)[1-6p(1-p)].}
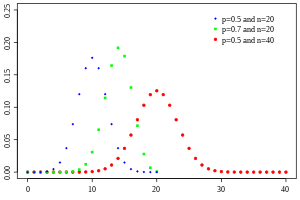
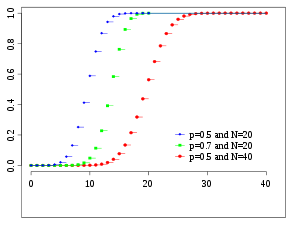
n
=
6
{\displaystyle n=6}
p
=
0.5
{\displaystyle p=0.5}
二项分布 及其正态近似标准二项分布
X
′
=
X
−
n
p
n
p
(
1
−
p
)
{\displaystyle X'={\frac {X-np}{\sqrt {np(1-p)}
在
n
→
∞
{\displaystyle \,n\to \infty \,}
趋近 于标准正态分布 。这一结果称作棣莫弗-拉普拉斯定理 中心极限定理 的特殊形式。基于这一定理可以得到
Pr
(
α
<
X
−
n
p
n
p
(
1
−
p
)
<
β
)
→
Φ
(
β
)
−
Φ
(
α
)
,
{\displaystyle \Pr(\alpha <{\frac {X-np}{\sqrt {np(1-p)}<\beta )\to \Phi (\beta )-\Phi (\alpha ),}
其中
Φ
{\displaystyle \,\Phi \,}
累积分布函数 。
正态分布为连续概率分布 ,在近似二项分布这类离散概率分布时,可将端点向外偏移
0.5
{\displaystyle \,0.5\,}
Pr
(
X
≤
k
)
≈
Φ
(
k
+
0.5
−
n
p
n
p
(
1
−
p
)
)
,
{\displaystyle \Pr(X\leq k)\approx \Phi \left({\frac {k+0.5-np}{\sqrt {np(1-p)}\right),}
从而提升近似的准确性,这种技巧称作连续性校正 经验法则 ,例如要求
n
p
(
1
−
p
)
>
9
{\displaystyle \,np(1-p)>9\,}
p
≤
0.5
{\displaystyle \,p\leq 0.5\,}
n
p
>
5
{\displaystyle \,np>5\,}
p
>
0.5
{\displaystyle \,p>0.5\,}
n
(
1
−
p
)
>
5
{\displaystyle \,n(1-p)>5\,}
当
n
→
∞
,
p
→
0
{\displaystyle \,n\to \infty ,p\to 0\,}
n
p
{\displaystyle \,np\,}
n
p
{\displaystyle \,np\,}
泊松分布 。以此为基础可以得到
Pr
(
X
≤
k
)
≈
e
−
n
p
∑
j
=
0
k
(
n
p
)
j
j
!
.
{\displaystyle \Pr(X\leq k)\approx e^{-np}\sum _{j=0}^{k}{\frac {(np)^{j}{j!}.}
二项分布与其泊松近似之间的绝对误差存在上界。若随机变量
X
{\displaystyle \,X\,}
n
,
p
{\displaystyle \,n,p\,}
Y
{\displaystyle \,Y\,}
n
p
{\displaystyle \,np\,}
∑
k
=
0
∞
‖
Pr
(
X
=
k
)
−
Pr
(
Y
=
k
)
‖
≤
min
{
2
n
p
2
,
3
p
}
.
{\displaystyle \sum _{k=0}^{\infty }\|\Pr(X=k)-\Pr(Y=k)\|\leq \min\{2np^{2},3p\}.}
通常参数
n
{\displaystyle \,n\,}
X
{\displaystyle \,X\,}
p
{\displaystyle \,p\,}
X
{\displaystyle \,X\,}
x
{\displaystyle \,x\,}
矩估计 和最大似然估计 对参数
p
{\displaystyle \,p\,}
估计量 均为
x
n
{\displaystyle \,{\frac {x}{n}\,}
无偏 的。
参数
p
{\displaystyle \,p\,}
贝叶斯估计量 先验分布 。若使用连续型均匀分布 作为先验分布,即假设
0
{\displaystyle \,0\,}
1
{\displaystyle \,1\,}
区间 包含
p
{\displaystyle \,p\,}
p
^
=
x
+
1
n
+
2
.
{\displaystyle {\widehat {p}={\frac {x+1}{n+2}.}
这被称作拉普拉斯–贝叶斯估计量 皮埃尔-西蒙·拉普拉斯 用于估计在太阳 连续升起
n
{\displaystyle \,n\,}
若使用参数为
α
,
β
{\displaystyle \,\alpha ,\beta \,}
贝塔分布 作为先验分布,则后验均值估计量为
p
^
=
α
+
x
+
1
α
+
β
+
n
+
2
.
{\displaystyle {\widehat {p}={\frac {\alpha +x+1}{\alpha +\beta +n+2}.}
采用贝塔分布作为先验分布时,后验分布 亦是贝塔分布,即贝塔分布为二项分布的共轭先验 。
若要对参数
p
{\displaystyle \,p\,}
区间 形式给出估计,通过求解
∑
j
=
x
n
(
n
j
)
p
L
j
(
1
−
p
L
)
n
−
j
=
α
2
,
{\displaystyle \sum _{j=x}^{n}{n \choose j}p_{L}^{j}(1-p_{L})^{n-j}={\frac {\alpha }{2},}
∑
j
=
0
x
(
n
j
)
p
U
j
(
1
−
p
U
)
n
−
j
=
α
2
,
{\displaystyle \sum _{j=0}^{x}{n \choose j}p_{U}^{j}(1-p_{U})^{n-j}={\frac {\alpha }{2},}
所得的区间
(
p
L
,
p
U
)
{\displaystyle \,(p_{L},p_{U})\,}
1
−
α
{\displaystyle \,1-\alpha \,}
置信区间 ,称作克洛珀-皮尔逊区间(Clopper-Pearson interval )。
正态分布可以用于推导近似的置信区间。若用
λ
α
/
2
{\displaystyle \,\lambda _{\alpha /2}\,}
1
−
α
2
{\displaystyle \,1-{\frac {\alpha }{2}\,}
分位数 ,即
Φ
(
λ
α
/
2
)
=
1
−
α
2
{\displaystyle \,\Phi (\lambda _{\alpha /2})=1-{\frac {\alpha }{2}\,}
x
n
±
λ
α
/
2
n
x
n
(
1
−
x
n
)
.
{\displaystyle {\frac {x}{n}\pm {\frac {\lambda _{\alpha /2}{\sqrt {n}{\sqrt {\frac {x}{n}\left(1-{\frac {x}{n}\right)}.}
Blyth, C. R. Approximate Binomial Confidence Limits . Journal of the American Statistical Association. 1986, 81 : 843–855. doi:10.1080/01621459.1986.10478343 (英语) . Chew, V. Point Estimation of the Parameter of the Binomial Distribution. The American Statistician. 1971, 25 (5): 47–50. doi:10.1080/00031305.1971.10477305 (英语) . Feller, W. An Introduction to Probability Theory and Its Applications, Volume 1, Third Edition. Wiley. 1968. ISBN 0-471-25708-7(英语) . Hald, A. A History of Probability and Statistics and Their Applications before 1750. Wiley. 2003. ISBN 0-471-47129-1(英语) . Hamza, K. The Smallest Uniform Upper Bound on the Distance Between the Mean and the Median of the Binomial and Poisson Distributions. Statistics and Probability Letters. 1995, 23 : 21–25. doi:10.1016/0167-7152(94)00090-U (英语) . Johnson, N. L.; Kemp, A. W.; Kotz, S. Univariate Discrete Distributions, Third Edition. Wiley. 2005. ISBN 0-471-27246-9(英语) . Kaas, R.; Buhrman, J. M. Mean, Median and Mode in Binomial Distributions. Statistica Neerlandica. 1980, 34 (1): 13–18. doi:10.1111/j.1467-9574.1980.tb00681.x (英语) . Schader, M.; Schmid, F. Two Rules of Thumb for the Approximation of the Binomial Distribution by the Normal Distribution. The American Statistician. 1989, 43 (1): 23–24. doi:10.1080/00031305.1989.10475601 (英语) . Sheu, S. S. The Poisson Approximation to the Binomial Distribution . The American Statistician. 1984, 38 (3): 206–207. doi:10.1080/00031305.1984.10483202 (英语) . Stigler, S. M. The History of Statistics: The Measurement of Uncertainty before 1900 . Harvard University Press. 1986. ISBN 0-674-40340-1(英语) .
離散單變量
有限支集 無限支集
beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Flory–Schulz Gauss–Kuzmin 幾何分佈 对数分布 mixed Poisson 负二项分布 Panjer parabolic fractal 卜瓦松分布 Skellam Yule–Simon zeta
連續單變量
混合單變量
联合分布
Discrete: Ewens multinomial Continuous: 狄利克雷分布
multivariate Laplace 多元正态分布 multivariate stable multivariate t normal-gamma 随机矩阵 LKJ 矩阵正态分布 matrix t matrix gamma 威沙特分佈
定向統計
循環單變量定向統計 圆均匀分布 univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped asymmetric Laplace wrapped Lévy 球形雙變量 Kent 環形雙變量 bivariate von Mises 多變量 von Mises–Fisher Bingham 退化分布 和奇異分佈 其它
Circular 复合泊松分布 elliptical exponential natural exponential location–scale Maximum entropy Mixture Pearson Tweedie Wrapped















































































![{\displaystyle \mu '_{r}=E[X^{r}]=\sum _{j=0}^{r}{\frac {S(r,j)n!p^{j}{(n-j)!},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9eb616ff48171dc34a4694e4951109f642940d8e)







![{\displaystyle \mu _{4}=3[np(1-p)]^{2}+np(1-p)[1-6p(1-p)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afc6efa1ae3b379bf77653d9627e8a7d86a9060a)