Rozkład jednostajny ciągły Rozkład jednostajny ciągły
Gęstość prawdopodobieństwa Dystrybuanta Parametry a , b ∈ ( − ∞ , ∞ ) {\displaystyle a,b\in (-\infty ,\infty )}
Nośnik a ⩽ x ⩽ b {\displaystyle a\leqslant x\leqslant b}
Gęstość prawdopodobieństwa 1 b − a dla a ⩽ x ⩽ b 0 dla x < a lub x > b {\displaystyle {\begin{matrix}{\frac {1}{b-a}&{\text{dla }a\leqslant x\leqslant b\\\\0&{\text{dla }x<a{\text{ lub }x>b\end{matrix}
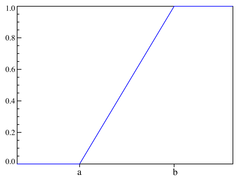
Dystrybuanta 0 dla x < a x − a b − a dla a ⩽ x < b 1 dla x ⩾ b {\displaystyle {\begin{matrix}0&{\text{dla }x<a\\{\frac {x-a}{b-a}&~~~~~{\text{dla }a\leqslant x<b\\1&{\text{dla }x\geqslant b\end{matrix}
Wartość oczekiwana (średnia)
a + b 2 {\displaystyle {\frac {a+b}{2}
Mediana a + b 2 {\displaystyle {\frac {a+b}{2}
Moda każda wartość w przedziale [ a , b ] {\displaystyle [a,b]}
Wariancja ( b − a ) 2 12 {\displaystyle {\frac {(b-a)^{2}{12}
Współczynnik skośności 0 {\displaystyle 0}
Kurtoza − 6 5 {\displaystyle -{\frac {6}{5}
Entropia ln ( b − a ) {\displaystyle \ln(b-a)}
Funkcja tworząca momenty e t b − e t a t ( b − a ) {\displaystyle {\frac {e^{tb}-e^{ta}{t(b-a)}
Funkcja charakterystyczna e i t b − e i t a i t ( b − a ) {\displaystyle {\frac {e^{itb}-e^{ita}{it(b-a)}
Rozkład jednostajny (zwany też jednorodnym , równomiernym , prostokątnym albo płaskim ) – ciągły rozkład prawdopodobieństwa , dla którego gęstość prawdopodobieństwa w przedziale od, a do b jest stała i różna od zera, a poza nim równa zeru. Istnieje też wersja dyskretna tego rozkładu oraz uogólnienie na dowolne nośniki .
Ponieważ rozkład jest ciągły, nie ma większego znaczenia czy punkty, a i b włączy się do przedziału czy nie. Rozkład jest określony parą parametrów, a i b, takich że b>a.
Podstawiając, a i b wyrażone jako funkcje wartości oczekiwanej i wariancji do wzoru na gęstość prawdopodobieństwa rozkładu jednostajnego powyżej, można ją też zapisać jako:
p ( x ) = { 0 dla x < μ − 3 σ 1 2 3 σ dla μ − 3 σ ⩽ x ⩽ μ + 3 σ 0 dla x > μ + 3 σ {\displaystyle p(x)={\begin{cases}0&{\text{dla }\ x<\mu -{\sqrt {3}\sigma \\{\frac {1}{2{\sqrt {3}\sigma }&{\text{dla }\ \mu -{\sqrt {3}\sigma \leqslant x\leqslant \mu +{\sqrt {3}\sigma \\0&{\text{dla }\ x>\mu +{\sqrt {3}\sigma \end{cases}
Rozkłady statystyczne
Rozkłady ciągłe Rozkłady dyskretne
The article is a derivative under the Creative Commons Attribution-ShareAlike License .
A link to the original article can be found here and attribution parties here
By using this site, you agree to the Terms of Use . Gpedia ® is a registered trademark of the Cyberajah Pty Ltd






![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)






