Distribució binomial
 | |
Funció de distribució de probabilitat 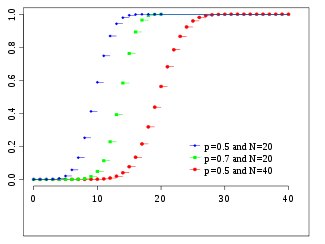 | |
| Tipus | Distribució binomial de Poisson, Panjer distribution (en) |
|---|---|
| Paràmetres | nombre d'assaigs (sencer) probabilitat d'èxit (real) |
| Suport | |
| FD | |
| Esperança matemàtica | |
| Mediana | o [1] |
| Moda | o |
| Variància | |
| Coeficient de simetria | |
| Curtosi | |
| Entropia | |
| FGM | |
| FC | |
| Mathworld | BinomialDistribution |
En Teoria de la probabilitat i en estadística, una variable aleatòria es diu que té una distribució binomial de paràmetres i si representa el nombre d'èxits en repeticions independents d'una prova que té probabilitat d'èxit . Per exemple, tirem 10 vegades un dau ordinari i comptem quantes vegades surt un 6; en aquest cas l'èxit és "treure un 6", i la variable que compta el nombre de sisos té una distribució binomial de paràmetres i .
La distribució binomial és la base de la popular prova binomial de significació estadística.[2]
Va ser proposada pel matemàtic i físic suís Jacob Bernoulli.[3]
Distribució de Bernoulli
Les distribucions binomials s'inscriuen en el marc de referència de les distribucions de Bernoulli. S'anomena experiència de Bernoulli aquell experiment aleatori del qual només s'estudia la verificació o no d'un esdeveniment que pot donar-se amb probabilitat La realització de l'esdeveniment s'anomena èxit. S'acostuma a representar la probabilitat del complementari (no ), la realització del qual s'anomena fracàs, per és clar que
Així, un experiment o experiència de Bernoulli es caracteritza per ser dicotòmic, és a dir, només són possibles dos resultats: èxit o fracàs.
Exemples d'experiències de Bernoulli
- Es llança una moneda, l'esdeveniment A podria ser "que surti cara".
- En una bossa hi ha boles blanques, negres i vermelles. traiem una bola i mirem si és de color blanc o no. L'esdeveniment A podria ser "treure bola blanca".
- En un referèndum amb possibles respostes Sí o No, l'esdeveniment A podria ser "que surti Sí".
Distribució binomial
La distribució binomial és una distribució de probabilitat discreta que fa el recompte del nombre de vegades que es verifica l'èxit (realització de l'esdeveniment ) quan es repeteix vegades, de forma independent i en les mateixes condicions, una experiència de Bernouilli.
Per n = 1, la distribució binomial és una distribució de Bernoulli.
Designem per X la variable aleatòria que mesura el nombre d'èxits que s'han produït en els n experiments. Per indicar que segueix una distribució binomial de paràmetres n i p , s'escriu:
Exemples
Les següents situacions són exemples d'experiments que poden modelitzar per aquesta distribució:
- Es llança un dau deu vegades i es compta el nombre de sisos obtinguts: X ~ B(10, 1/6)
- Es llança una moneda dues vegades i es compta el nombre de cares obtingudes, tenim
- Una partícula es mou unidimensionalment amb probabilitat de moure's una unitat de distància cap enrere i de moure's una unitat cap endavant. Després de moviments, el nombre de vegades que s'ha mogut cap endavant és una variable binomial .
Propietats característiques
Mitjana i Variància
Sigui una variable aleatòria binomial de paràmetres i .
Això es dedueix per la linealitat de l'esperança, ja que X és la suma de n variables aleatòries de Bernoulli idèntiques, cadascuna d'elles amb esperança p. És a dir, si són variables aleatòries iguals (i independents) de Bernoulli amb paràmetre p, aleshores i, atès que tindrem que D'altra banda, per a una variable de Bernoulli, d'on Llavors, de la independència de , es dedueix que
Funció de probabilitat
Sigui una variable aleatòria binomial de paràmetres i . Aleshores la probabilitat d'obtenir exactament èxits en repeticions (proves) independents de Bernouilli és:
on és el coeficient binomial.
Així, la funció de probabilitat de és
Funció de distribució
on denota la part entera de .
Fites de les cues
Per k ≤ np, es poden derivar fites superiors per la cua inferior de la funció de distribució acumulada , la probabilitat que hi hagi com a màxim k successos. Com que , també es poden interpretar aquestes fites per a la cua superior de la funció de distribució per k ≥ np.
La desigualtat de Hoeffding dóna la fita simple
que no és, tanmateix, gaire forta. En particular, quan p = 1, s'obté F(k;n,p) = 0 (per a k i n fixes amb k < n), però la fita de Hoeffding dóna una constant positiva.
S'obté una fita més exacta mitjançant la fita de Chernoff:[4]
on D(a || p) és l'entropia relativa (o divergència Kullback-Leibler) entre una moneda-ai una moneda-p (és a dir entre Bernoulli(a) i Bernoulli(p) distribution):
Asimptòticament, aquesta fita és raonablement exacta; vegi's [4] per més detalls.
També es poden obtenir fites inferiors de la cua , conegudes com fites anti-concentració. Aproximant el coeficient binomial amb l'aproximació de Stirling es pot demostrar que[5]
que implica la fita més simple però menys exacta:
Per p = 1/2 i k ≥ 3n/8 amb n parell, es pot fer que el denominador sigui constant:[6]
Exemple
Suposem que tenim una moneda trucada amb probabilitat 0.3 que surti cara. La probabilitat que surtin 4 cares en 6 llançaments és
Aproximació de la distribució binomial per les distribucions de Poisson i normal
Si tendeix a infinit i és tal que , llavors la distribució d'una variable aleatòria binomial de paràmetres i tendeix a una distribució de Poisson de paràmetre .
D'altra banda, pel teorema central del límit, quan n és gran (normalment s'exigeix que ) la distribució binomial es pot aproximar mitjançant la distribució normal.
Distribucions relacionades
Suma de binomials
Si X ~ B(n, p) i Y ~ B(m, p) són variables binomials independents amb la mateixa probabilitat p, llavors X + Y és també una variable binomial; la seva distribució és Z = X \+ Y ~ B(n + m, p):[7]
Es pot considerar una variable aleatòria distribuïda de forma binomial X ~ B(n, p) com la suma de n variables aleatòries distribuïdes segons Bernoulli. Així doncs, la suma de les variables aleatòries binomials X ~ B(n, p) i Y ~ B(m, p) és equivalent a la suma de n + m variables aleatòries de Bernoulli, és a dir Z = X + Y ~ B(n + m, p). També es pot demostrar això directament utilitzant la regla de la suma.
No obstant això, si X i Y no tenen la mateixa probabilitat p, llavors la variància de la suma serà més petita que la variància de la variable binomial distribuïda com B(n + m, p).
Distribució binomial de Poisson
La distribució binomial és un cas particular de la distribució binomial de Poisson, que és la distribució de una suma de n assajos de Bernoulli independents i no idèntics B(pi).[8]
Ràtio de dues distribucions binomials
Aquest resultat va ser derivat per primer cop per Katz i coautors l'any 1978.[9]
Siguin X ~ B(n, p1) i Y ~ B(m, p2) independents. Sigui T = (X/n) / (Y/m).
Llavors log(T) està distribuït aproximadament de forma normal amb mitjana log(p1/p2) i variància ((1/p1) − 1)/n + ((1/p2) − 1)/m.
Distribució de Bernoulli
La distribució de Bernoulli és un cas particular de la distribució binomial, amb n = 1. Simbòlicament, X ~ B(1, p) té el mateix significat que X ~ Bernoulli(p). En canvi, la distribució binomial, B(n, p), és la distribució de la suma de n assajos de Bernoulli independents, Bernoulli(p), cadascun amb la mateixa probabilitat p.[10]
Aproximació de Poisson
La distribució binomial convergeix a la distribució de Poisson a mesura que el nombre d'assajos tendeix a infinit mentre que el producte np convergeix a un límit finit. Per tant, es pot utilitzar una distirbució de Poisson amb paràmetre λ = np per aproximar B(n, p) de la distribució binomial si n és prou gran i p és prou petit. Segons la regla del polze, aquesta aproximació és bona si n ≥ 20 i p ≤ 0.05[11] tal que np ≤ 1, o si n > 50 i p < 0.1 tal que np < 5,[12] o si n ≥ 100 i np ≤ 10.[13][14]
Sobre la precisió de l'aproximació de Poisson, vegi's Novak,[15] capítol 4, i les referències que s'hi citen.
Propietats reproductives
Donades m variables binomials independents , i = 1, ..., m, de paràmetres i , respectivament, la seva suma S és també una variable binomial, de paràmetres i , és a dir,
Referències
- ↑ Hamza, K. (1995). The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions. Statistica & Probability Letters. 23 21-25.
- ↑ Westland, J. Christopher. Audit Analytics: Data Science for the Accounting Profession. Chicago, IL, USA: Springer, 2020, p. 53. ISBN 978-3-030-49091-1.
- ↑ Cervigon, Francesc La-Roca. Estadística aplicada a les ciències socials. Universitat de València, 2011-11-28, p. 191. ISBN 978-84-370-8650-7.
- ↑ 4,0 4,1 Arratia, R.; Gordon, L. «Tutorial on large deviations for the binomial distribution». Bulletin of Mathematical Biology, vol. 51, 1, 1989, pàg. 125–131. DOI: 10.1007/BF02458840. PMID: 2706397.
- ↑ Robert B. Ash. Information Theory. Dover Publications, 1990, p. 115. ISBN 9780486665214.
- ↑ Matoušek, J.; Vondrak, J. «The Probabilistic Method». lecture notes. Arxivat de l'original el 2022-10-09.
- ↑ Dekking, F.M.; Kraaikamp, C.; Lopohaa, H.P. [et al.].. A Modern Introduction of Probability and Statistics. 1. Springer-Verlag London, 2005. ISBN 978-1-84628-168-6.
- ↑ Wang, Y. H. «On the number of successes in independent trials». Statistica Sinica, vol. 3, 2, 1993, pàg. 295–312.
- ↑ Katz, D.; Baptista, J.; Azen, S. P.; Pike, M. C. «Obtaining confidence intervals for the risk ratio in cohort studies». Biometrics, vol. 34, 3, 1978, pàg. 469–474. DOI: 10.2307/2530610. JSTOR: 2530610.
- ↑ Taboga, Marco. «Lectures on Probability Theory and Mathematical Statistics». statlect.com. [Consulta: 18 desembre 2017].
- ↑ «12.4 – Approximating the Binomial Distribution | STAT 414», 28-03-2023. Arxivat de l'original el 2023-03-28. [Consulta: 8 octubre 2023].
- ↑ Chen, Zac. H2 mathematics handbook. 1. Singapore: Educational publishing house, 2011, p. 348. ISBN 9789814288484.
- ↑ NIST/SEMATECH, "6.3.3.1. Counts Control Charts", e-Handbook of Statistical Methods.
- ↑ «The Connection Between the Poisson and Binomial Distributions», 13-03-2023. Arxivat de l'original el 2023-03-13. [Consulta: 8 octubre 2023].
- ↑ Novak S.Y. (2011) Extreme value methods with applications to finance. London: CRC/ Chapman & Hall/Taylor & Francis. ISBN 9781-43983-5746.





























![{\displaystyle \mathbb {E} [X]=np\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bb48ee9599c156235bc915dc987ce20a5af6f59)


![{\displaystyle E[X_{i}]=p\cdot 1+q\cdot 0=p,\ i=1,\dots ,n,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61cc4e194e0726c316bb182440b76bef1d92cd66)
![{\displaystyle \operatorname {E} [X]=\operatorname {E} [X_{1}+\cdots +X_{n}]=\operatorname {E} [X_{1}]+\cdots +\operatorname {E} [X_{n}]=p+\cdots +p=np.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f238d520c68a1d1b9b318492ddda39f4cc45bb8)
![{\displaystyle E[X_{i}^{2}]=p\cdot 1^{2}+q\cdot 0^{2}=p,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/289d82e40dc532168d92c7d0e56cbe8c3c78fab8)


![{\displaystyle {\text{Var}[X]=np(1-p).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e745dea0524daf4902c59ad95999610329036e5)





![{\displaystyle F(x)=\Pr(X\leq x)={\begin{cases}0,&{\text{si}\,x<0,\\\displaystyle {\sum _{i=0}^{\lfloor x\rfloor }{n \choose i}p^{i}(1-p)^{n-i},&{\text{si}\,x\in [0,n],\\1,&{\text{si}\,x>n.\end{cases}](https://wikimedia.org/api/rest_v1/media/math/render/svg/477eabf845c1cad184dbaad875debc138fcd7546)
![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
















![{\displaystyle {\begin{aligned}\operatorname {P} (Z=k)&=\sum _{i=0}^{k}\left[{\binom {n}{i}p^{i}(1-p)^{n-i}\right]\left[{\binom {m}{k-i}p^{k-i}(1-p)^{m-k+i}\right]\\&={\binom {n+m}{k}p^{k}(1-p)^{n+m-k}\end{aligned}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38fc38e9a5e2c49743f45b4dab5dae6230ab2ad5)




